谈谈如何实现具备 ACID 事务的分布式 KV 存储

发表于 更新于 Disqus：

F1/Spanner 的论文于 2012 年发表，至今仍是世界上最先进的、规模最大的分布式数据库架构，毫无疑问对现代数据库设计产生了深远影响。其最大的亮点莫过于 TrueTime API，凭借原子钟和 GPS 的加持在全球范围实现了单调递增的时间戳，从而达到外部一致性；其次则是验证了分布式 MVCC 的高性能实现，为业界指明一条发展方向。

不过，论文对存储层实现只作了模糊的阐述：原文中说到 tablet 的实现类似于 Bigtable（复用了不少 Bigtable 的代码），底层基于 Colossus —— 继承 GFS 的下一代分布式文件系统。可以确定的一点是，存储层要为 read-only 和 read-write 事务提供支持：

  • read-only 事务: 读取最新或给定时间戳 的快照，也就是 snapshot read
  • read-write 事务：读取事务开始时间戳 的快照，而写入操作在提交时间戳 生效

本文从 F1/Spanner 论文出发，结合开源实现 TiDB 和 CockroachDB，谈谈如何设计一个具备 ACID 事务存储层。本文假设读者阅读过原论文 Spanner: Google's Globally-Distributed Database。

数据的 KV 表示

F1/Spanner 对外提供（半）关系型数据模型：每张表定义了一个或多个主键列，以及其他的非主键列。这和我们熟知的 SQL 关系型模型几乎一摸一样，唯一的不同是 schema 定义中必须含有主键。

F1/Spanner 早期的设计中大量复用了 BigTable（开源实现即 HBase）的代码。回忆一下 BigTable 的数据模型：每一条数据包含 (Key, Column, Timestamp) 三个维度，满足我们需要的 MVCC 特性。从 BigTable 开始的确是个不错的选择。

不过，从性能上考虑 Bigtable 毕竟是分布式的 KV 存储系统，在存储这一层我们大可不用搞的那么复杂，分布式的问题例如 scale-out 和 replication 应当留给上层的 sharding 机制和 Paxos 解决。事实上，一个单机的存储引擎足矣。

Google 自家的 LSM-Tree + SSTable 的实现 LevelDB 是个可选项。它接口非常简单，是一个标准的 KV 存储，可以方便的在它基础上实现我们想要的数据模型。主要接口其实就是两个：

  • Write(WriteBatch *) 原子地写入一个 WriteBatch，包含一组 Put(K, V) 和 Delete(K) 操作
  • Iterator() 及 Seek() 从指定位置开始顺序扫描读取 (K, V) 数据

如何实现列和时间戳呢？举个例子，有如下数据表 Accounts。在数据库中，主键索引通常也是唯一的聚簇索引，它存放了真实的数据，而我们暂时不考虑其他索引。

1
2
3
4
| UserID (PK) | Balance | LastModified |
|-------------|---------|--------------|
| Alice       | 20      | 2018-02-20   |
| Bob         | 10      | 2018-02-01   |

Spanner 内部使用 MVCC 机制，所以还有一个隐藏的时间戳维度：

1
2
3
4
5
| UserID | Timestamp | Balance | LastModified |
|--------|-----------|---------|--------------|
| Alice  | 103       | 20      | 2018-02-20   |
| Alice  | 101       | 15      | 2018-01-20   |
| Bob    | 102       | 10      | 2018-02-01   |

上述数据表用 KV 模型存储，可以表示为

1
2
3
4
5
6
7
8
| Key                             | Value      |
|---------------------------------|------------|
| Accounts/Alice/Balance/103      | 20         |
| Accounts/Alice/Balance/101      | 15         |
| Accounts/Alice/LastModified/103 | 2018-02-20 |
| Accounts/Alice/LastModified/101 | 2018-01-20 |
| Accounts/Bob/Balance/102        | 10         |
| Accounts/Bob/LastModified/102   | 2018-02-01 |

上表中 / 表示一个分隔符，真实情况要更复杂。Key 这样编码：从左到右依次是表名（因为可以有不止一张表）、主键字段、列的标识符、时间戳（通常倒序排列，Tips. 取反即可）。Value 则对应原表中的数据。

显然，对于半关系型数据一定能由表名、主键字段、列名唯一地确定一个值，所以这个编码方式能满足我们的要求。

如果一张表只有主键怎么办呢？这种情况下可以为每个主键填充一个 placeholder 的 value 即可。

事务的原子性

众所周知，事务具有四个特性：原子性（Atomicity）、一致性（Consistency）、隔离性（Isolation）、持久性（Durability）。其中一致性和持久性其实是数据库系统的特性，对于事务，我们更多讨论的是原子性和隔离性。

对于存储层而言，为上层提供原子性 commit 的接口是必须的功能。如何在 KV 存储的基础上实现原子性呢？以下思路是一种常见的方案：

  1. 首先，准备一个开关，初始状态为 off，当我们把开关打开的那一刻，意味着 commit 生效可见；
  2. 将所有变更以一种可回滚的方式（e.g. 不能覆盖现有的值）写入存储中。开关同时决定了其它 reader 的视图，由于开关还是 off 状态，现在写入的变更不会被其它事务看到。
  3. 之后，写入开关状态为 on，标志着 commit 的成功，新数据生效，即所谓 commit point。这个写入操作本身的原子性由 LevelDB 保证。
  4. 最后，清除掉中间状态（比如第 2 步中的临时数据）并写入最终的数据。这一步可以异步的完成，因为在第 3 步中事实上 commit 已经成功了，无需等待。

保证原子性的关键在于 commit point。例如，在单机数据库中，commit point 是 commit 的 redo-log 写入磁盘的一瞬间；在 XA 两阶段提交中，commit point 是协调器将事务状态置为 Committed 的一瞬间。

在我们的存储中，commit point 也就是第 3 步的写入操作。如果提交过程意外终止在 commit point 之前，我们会在读取时发现第 2 步中的临时写入，然后轻松地清除它；如果意外终止在 commit point 之后，部分临时状态没有被清除，只需继续执行 4 即可。

上述只是一个解决问题的思路。具体的解决方案可以参考 Percolator 的事务实现。这同时也是 TiDB 的做法，CockroachDB 做法略有不同，但同样遵从这个模式。

Percolator 事务方案

Percolator 是 Google 早期的分布式事务解决方案，用于进行大规模增量数据处理。Percolator 在 BigTable 基础上基于 2PL 思想实现了分布式事务。这个算法很简单，你可以把它看作是是封装了一系列 BigTable 的 API 访问（本身无状态），所以可以容易地移植到 KV 存储模型上。

Percolator 事务模型基于单调递增的时间戳，来源于集群中唯一的 timestamp oracle。每个事务拥有提交时间戳 和开始时间戳 。Percolator 事务模型和之前说到的 write-read 事务一致：事务中总是读取 时的 snapshot，而写入则全部在 生效。这也意味着事务中所有写入都被 buffer 到最后进行，不支持类似于 read-write-read 这样的模式。

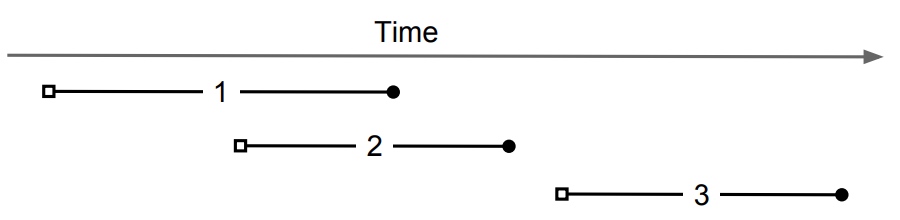
如图，事务 2 看到的是事务 1 提交前的状态，而事务 3 看到的是事务 1、2 提交后的状态。

Percolator 基于 BigTable 的事务实现如下：

除了数据本身（bal:data 列）以外，我们给数据再加上两列：lock 和 write。

  • write 列存放了一个指针，指向写入的 data 的时间戳
  • lock 列用于 2PL，加锁时也保存了 primary lock 的位置。

primary lock 不仅代表当前行的锁状态，还兼任上文中“开关”的作用。通常选取第一个写入的数据作为 primary lock。

以下表为例。表中 6: data @ 5 表示： 时事务提交，确定了 Bob 对应的值是 5: $10（所以推测出该事务 ）。其他事务读取时，为了避免读到 uncommitted 的数据，都会先从 write 列开始找，然后再读出其指向的 data。

现在，用户要从 Bob 账户里转 $7 给 Joe，为此必须开启一个事务。 时，转账事务开始，向 Bob 和 Joe 的 data 写入新的余额。

时，用户 commit 事务。事务的第一阶段（Prewrite）亦即是 2PL 的加锁阶段，先为 Bob 和 Joe 都加上锁。如下图所示，lock 不为空即代表加上了锁，其内容指向 primary lock 的位置。简单起见，不妨设第一条被锁的数据为 primary row。

下一步很关键：清除 primary row 的 lock 并向 write 列写入新 data 的位置。这也就是所谓 commit point，这个写入的成功或失败决定了事务提交成功与否：

  • 若写入成功，则代表整个事务成功。之后会遍历所有加锁的行，解除 lock 并向 write 列写入新的 data 位置。这样一来，其他事务就能读到当前事务写入的数据。
  • 否则，整个事务失败。之后会遍历所有加锁的行，解除 lock 并清除之前写入的 data，恢复原状。

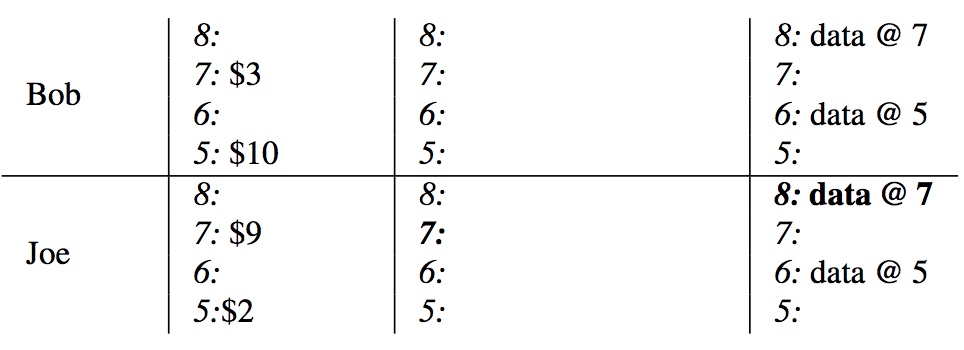
回到例子中，当 commit point 完成后，表的状态如下：

解除 Joe 的 lock 并向 write 列写入新 data 的位置，至此事务 commit 完成：

Commit point 这一步本身的原子性由 BigTable 行事务保证。对于 commit point 前后的其他操作，如果系统当机重启，恢复线程可以通过检查 commit point 操作的结果，来确定该 roll forward 还是 roll back。具体而言：

  • 通过 lock 找到 primary lock，如果已经解除，说明 commit point 已经完成，需要 roll forward 事务。
  • 否则，如果 primary lock 还在，说明 commit point 还没到，只能 roll back 事务。

于是，通过 2PL，我们成功地在 BigTable 的行级事务基础上实现了表级事务。

上述过程很容易的能映射到 KV 存储模型上。按照前一节描述的方法，将 lock 和 write 列都视作普通的列即可。这里不再赘述。

事务的隔离性

上述的讨论只考虑了单个事务的原子性保证——如何确保能从从中间状态恢复到未提交或已提交的状态，而没有考虑多线程并发的情况。如果同时有多个 client 在运行多个事务，如何保证严格互相隔离？（Serializable级别）

Percolator 是一个典型的 Snapshot Isolation 实现。Percolator 包含一个被称为 Strict-SI 的改进：在事务 commit 中，如果发现有一个高于 的版本出现，则放弃 commit。这能避免 lost update 问题。但是 write-skew 问题依然存在。

F1/Spanner 提供 Serializable 隔离性保证。相应的算法被称为 Serializable Snapshot Isolation (SSI)。

冲突图理论

首先对以上问题建模。考虑两个事务对同一条数据先后发生两次读或写操作，于是有 4 种情况：

  • Read-Read：这是OK的，它不会引起冲突；
  • Read-Write：后发生的操作覆盖了前一个读的数据，这是一种冲突；
  • Write-Read：读到另一个事务的写入，这是一种冲突。
  • Write-Write：即覆盖写，这是一种冲突。

上述三种冲突的情况，并不是一定会导致问题。举个例子：事务仅仅是覆盖了事务写入的数据，那么和仍然是符合 serializable 的，只要逻辑上认为发生在之后。

哪些情况会违反 serializable 呢？简单来说，如果冲突A迫使我们规定 先于 ，冲突B迫使我们规定 先于 ，这个因果关系就没法成立了，、无法以任何方式串行化。形式化的说：以所有事务 作为节点、以所有冲突 作为有向边构成一张有向图（这被称为冲突图或依赖图），如果这张图是有向无环图（DAG）则满足 serializable；否则（有环）不满足。

举个例子：

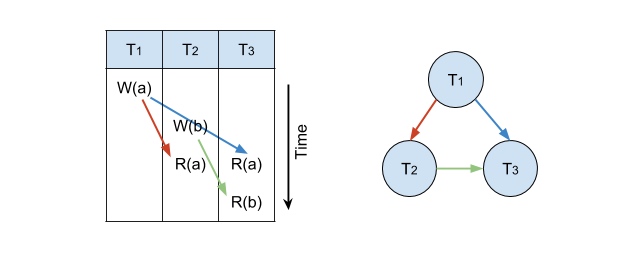
这是一个有向无环图，、、 满足 serializable。

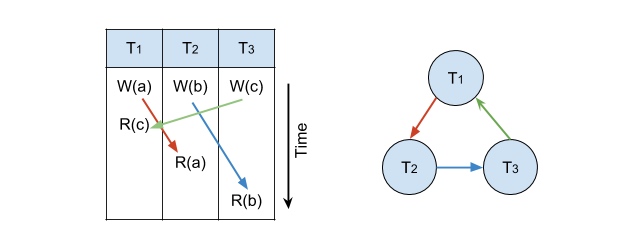
这是一个有环的图，、、 无法被串行化。

图论告诉我们，如果一张图是 DAG，等价于我们能为它进行拓扑排序，即给每个节点 assign 一个编号，使得所有边都是从编号小的节点指向编号大的。换而言之，如果我们能给每个节点 assign 一个这样的编号，则可以反推出原图是 DAG，进而证明 T 集合满足 serializable。

你可能已经隐约感觉到，这个编号和事务发生的顺序有关！事实上，编号代表 serializable 后的逻辑顺序，大多数时候，这个顺序和真实的时间顺序都是一致的。

Spanner 中强调自己满足的是比 serializable 更强的一致性：linearizable，说的就是不仅能序列化，而且序列化的“逻辑顺序”和时间上的“物理顺序”也一致。

Serializable Snapshot Isolation (SSI)

不妨把事务开始的时间戳 作为这个编号。将上述约束条件略微加强一些，就得到了简单有效的判断法则：对于冲突 ，如果时间戳满足 则允许发生；如果 则终止事务。

具体的来说，对于三种冲突，分别用以下方式处理：

  • Write-Read 冲突：感谢 MVCC，这是不会发生的，在 Percolator 的事务模型中，读操作一定是从一个过去时间点的 snapshot 上读取，而不会读到一个正在进行中事务的脏数据。（但是 MVCC 会引发另一个问题——staled read。见下文）

  • Write-Write 冲突：如果 Write 发生的时候，出现了一条 比较大的记录，则终止写事务。

Percolator 的 SI 实现使用了更强的约束：如果出现另一条比开始时间大的记录，无论其时间戳如何都会终止当前提交，这与 SSI 的机制有所区别。

由于 SI 无法完全避免 Read-Write 冲突（例如 write-skew 问题），所以在 Write-Write 冲突的处理上更为激进；但 SSI 已经解决了 Read-Write 冲突检测，不必用更强的约束。

  • Read-Write 冲突：为了知道 Write 和另一个事务的 Read 冲突，必须要以某种方式记录下所有被读过的数据、以及读取事务的 。这通常用范围锁（range lock）来实现——将所有查询的 TableScan 范围记录在内存中，如果某一条写入的数据满足某个 where 条件，则有必要检查一下二者的时间戳先后顺序。如果不满足上述判断法则，需要终止写事务。

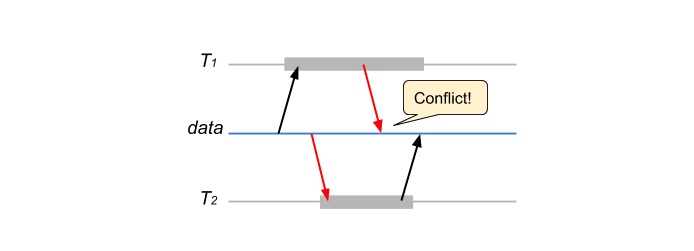
  • 由于 MVCC 的存在，Read-Write 冲突还有另一种形式： 的 Read 发生地更迟，但是由于 MVCC 它读到的是 写之前的值（staled read），而且这里 先于 从而构成 Read-Write 冲突。

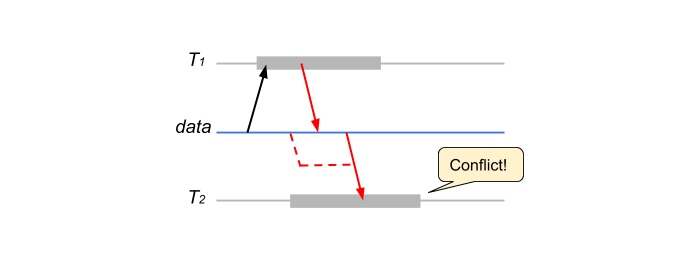
对此，一个简单的解决方案是：如果 发现 写入的中间数据（lock），则立即终止自己。经典 SSI 的做法是，在 commit 时如果发现 已经 commit 则放弃本次提交。

综上，通过给每个事务赋予一个时间戳，并保证每个冲突都符合时间戳顺序，达到 serializable 隔离级别。

总结

  1. 将 (Table, Key, Column, Timestamp) 作为 Key 的编码，从而把（半）关系型数据存储在 KV 引擎中；
  2. 用两阶段锁（2PL）的方式在 KV 引擎上实现事务的原子性提交。
  3. 禁止冲突违反时间戳先后顺序，从而保证 serializable 的隔离性。

References

  1. Spanner: Google's Globally-Distributed Database (OSDI'12)
  2. Large-scale Incremental Processing Using Distributed Transactions and Notifications - USENIX 2010 - Daniel Peng, Frank Dabek
  3. How CockroachDB Does Distributed, Atomic Transactions - Cockroach Labs
  4. Serializable, Lockless, Distributed: Isolation in CockroachDB - Cockroach Labs
  5. Designing Data‑Intensive Applications - Martin Kleppmann