Learned Index Structures 论文解读
数据库的索引和机器学习里的预测模型其实有一些相似之处,比如 B 树是把 key 映射到一个有序数组中的某个位置,Hash 索引是把 key 映射到一个无序数组中的某个位置,bitmap 是把 key 映射成是一个布尔值(存在与否)。
这些事,似乎拿预测模型都是可以做的。Yes, but...B 树那是精确的映射关系,和预测模型能一样吗?
所以这就是本论文 NB 的地方了,以上的想法是可以实现的。实验表明,在某些数据集上,用 RM-Index 预测模型代替 B 树之类的数据结构,可以提升 70% 的速度、并节约相当可观的空间。
范围索引
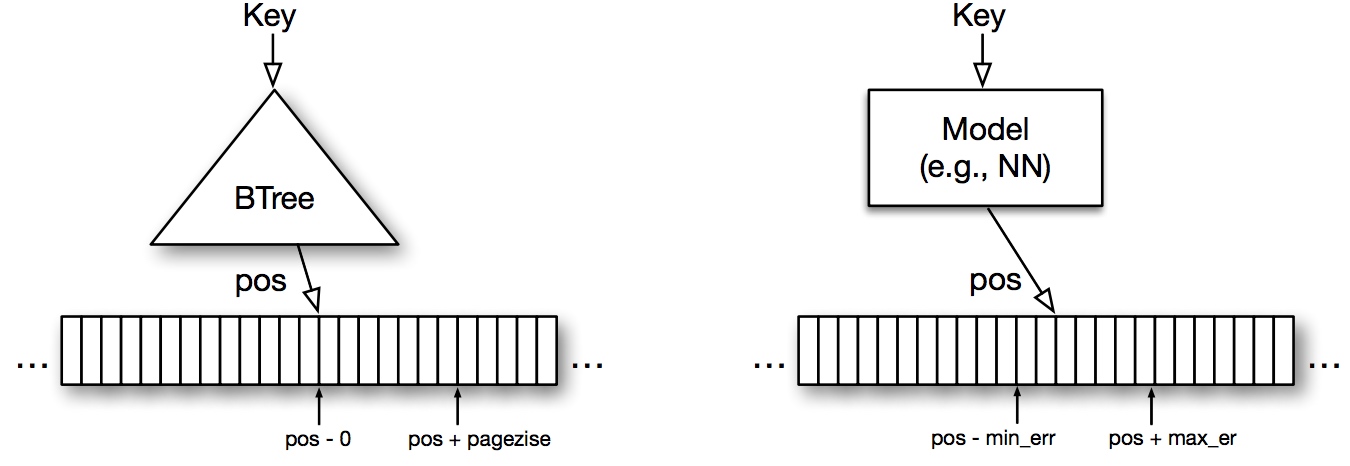
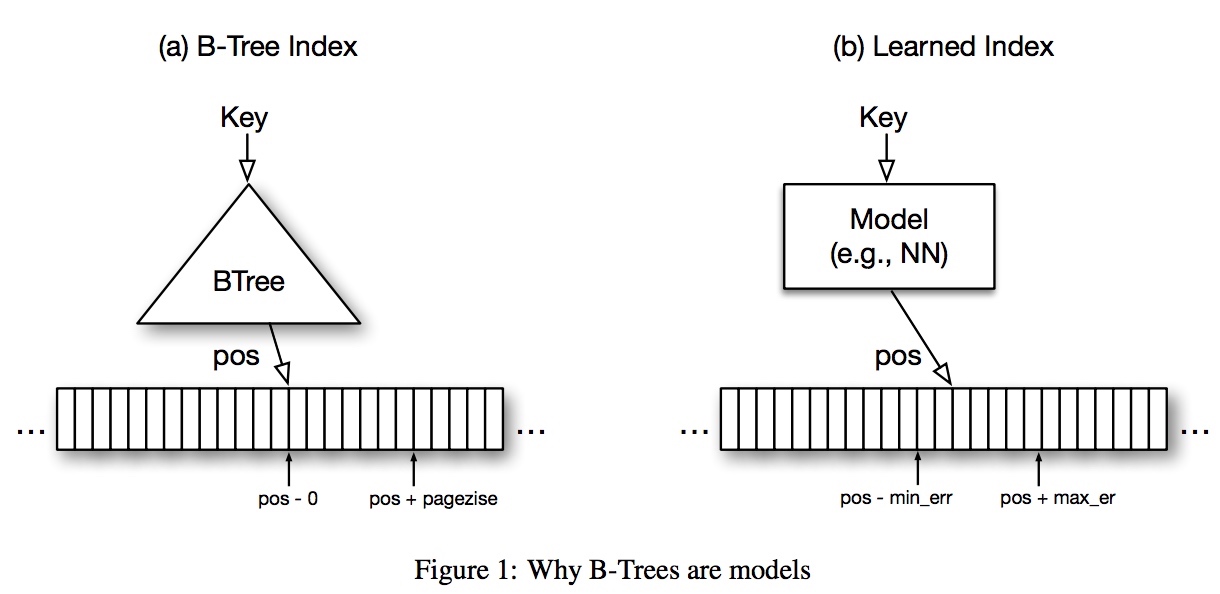
B 树和一个预测 model 是很相似的:
- B 树能定位某行数据所在的 page,可以看作是确定了一个区间:[pos, pos + pagesize]
- 预测模型也能做相似的事,假设我们把预测错误率成功 bound 在 min/max_err 以内,那么也就可以确定,数据位于区间 [pos - min_err, pos + max_err]
一图以概之:
于是问题变成,如何把预测错误率 bound 在 max_err 以内?
答案非常简单!通过训练。你可以把训练集的上的 error 降到多小都行,只要你模型的表现力足够强。这个问题和绝大多数机器学习的问题都不同,我们只要照顾好训练集(也就是被索引的数据)就可以了,没有测试集!当然也就不会有过拟合,模型的泛化能力是不用考虑的,比想象的简单吧!
说到模型表现力强,很容易想到神经网络。除此以外,NN 还带来了另一个好处,在 GPU(或其他专用芯片,比如 Google 的 TPU)上,NN 能获得惊人的计算速度。NN 的结构决定了它并行起来非常快,时间复杂度上把 \(O(\log{n})\) 的 B 树等甩在身后。
说到这里,我们来做个思维拓展:如果把 key 作为横轴,key 在有序数组中的位置 pos 作为纵轴,画出目标函数的曲线,那应该长成这个样子:
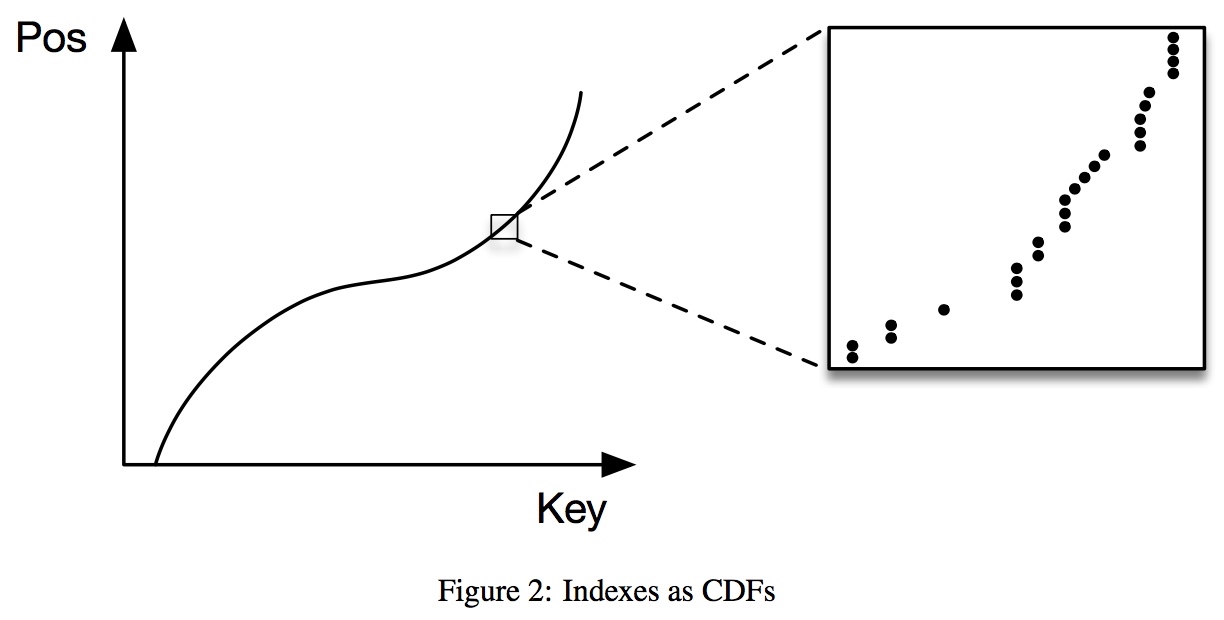
这是一个 CDF (累积分布函数,累积的是各个 key 对应数据的长度)。从这个角度看,无论是 B 树还是预测模型都是在拟合这个函数,只是 approach 完全不同。
这时候再回头看我们熟悉的 B 树,有没有一点顿悟—— Aha! 这不是就是决策树吗?
递归模型索引 RM-Index
以上已经说完了核心思想,接下来就是要找到一个合适的预测模型来代替 B 树。实验发现,直接上 DNN 效果并不好:单次计算代价太大,只能用 GPU(而调用 GPU 会产生不小的 overhead);而且网络很庞大,retrain(增删改)代价很大。
Naive 的预测模型之所以做的不好,一个重要原因是:把如此大量的数据每条误差 bound 在 min/max_err 之内,实在太难了(所谓 last mile 问题)。为解决这个问题,决策树给我们做了个很好的提示,如果一个模型解决不了问题,就再加几层。
举个例子:为 100M 记录训练一个足够精确的预测器太难,那就分成 3 层树状结构。根节点分类器把记录分出 100 份,每份大约有 1M 记录;第二层再分出 100 份,每份大约只剩 10K 记录;第三层再分出 100 份,每份大约有 100 条记录——假设 100 条纪录足够把误差在 min/max_err 之内。
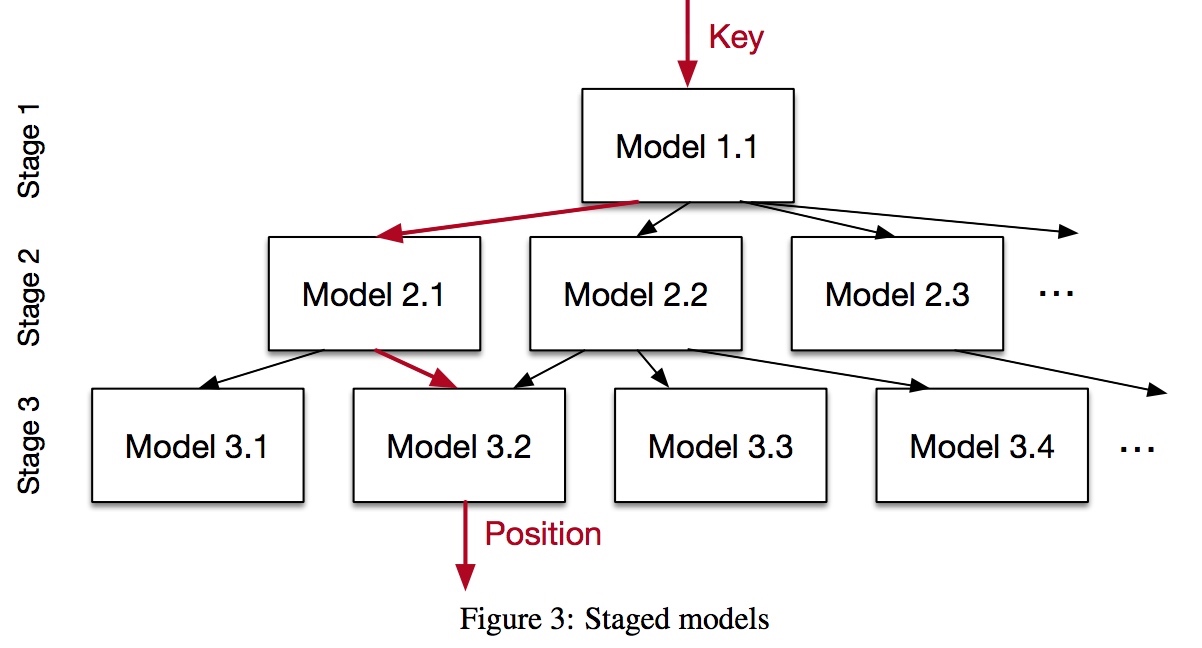
注意,上图并不是一棵树,例如 Model 2.1 和 2.2 都可以选择 Model 3.2 作为下一层的分类模型。
这样做的好处是,每层要做的事情简单多了(每层 precision gain = 100),模型可以变得简单得多。每个 NN 模型就像一个精通自己领域的专家,他只要学习某个很小子集的 keys 就可以了。这也同时解决了 last mile 难题,大不了为这一百左右个 keys 过拟合一下也无妨。
混合索引
上图中的三层网络结构还带来一个额外的优势:每个 Model 其实是独立的,我们可以用除了 NN 以外的预测方法代替之,包括线性回归等简单算法,甚至是 B 树。
事实上,最后选用了两种 Model:
- 简单的神经网络(0~2 层全连接的 hidden layer,ReLU 激发函数,每层最多 32 个神经元)
- 当叶节点的 NN 模型 error rate 超过阈值时,替换成 B 树
训练算法如下,

简单说就是:
- 固定整个 RM-Index 的结构,比如层数、每层 Model 数量等(可以用网格法调参);
- 用全部数据训练根节点,然后用根节点分类后的数据训练第二层模型,再用第二层分类后的数据训练第三层;
- 对于第三层(叶节点),如果 max_error 大于预设的阈值,就换成 B 树。
有了 Step 3,这个 RM-Index 的分类能力也就有了下界,即使面对纯噪声数据(毫无规律可循),至少能和 B 树保持差不多的性能。
索引的 keys 常常是字符串,而我们前文说的 NN 模型的输入是向量。Luckily,字符串向量化是 ML 里研究很多的一个课题了,这里不再讨论,有兴趣的可以看下原论文(抛砖引玉为主)。
测试结果
为了对比 RM-Index 和 B 树的性能,论文作者找了 4 个数据集,分别用 RM-Index 和 B 树作二级索引。
- Weblogs 数据集:访问时间 timestamp -> log entry (约 200M)
- Maps 数据集:纬度 longitude -> locations (约 200M)
- Web-documents 数据集:documents(字符串)-> document-id(约 10M)
- Lognormal 数据集:按对数正态分布随机生成的数据
测试中用了不同参数的 Learned Index 和 B 树,B 树也用了一个高度优化的实现。
总体来说,Size savings 都相当可观(下降 1~2 个数量级),而速度也有所优化,最多能快 1 倍。
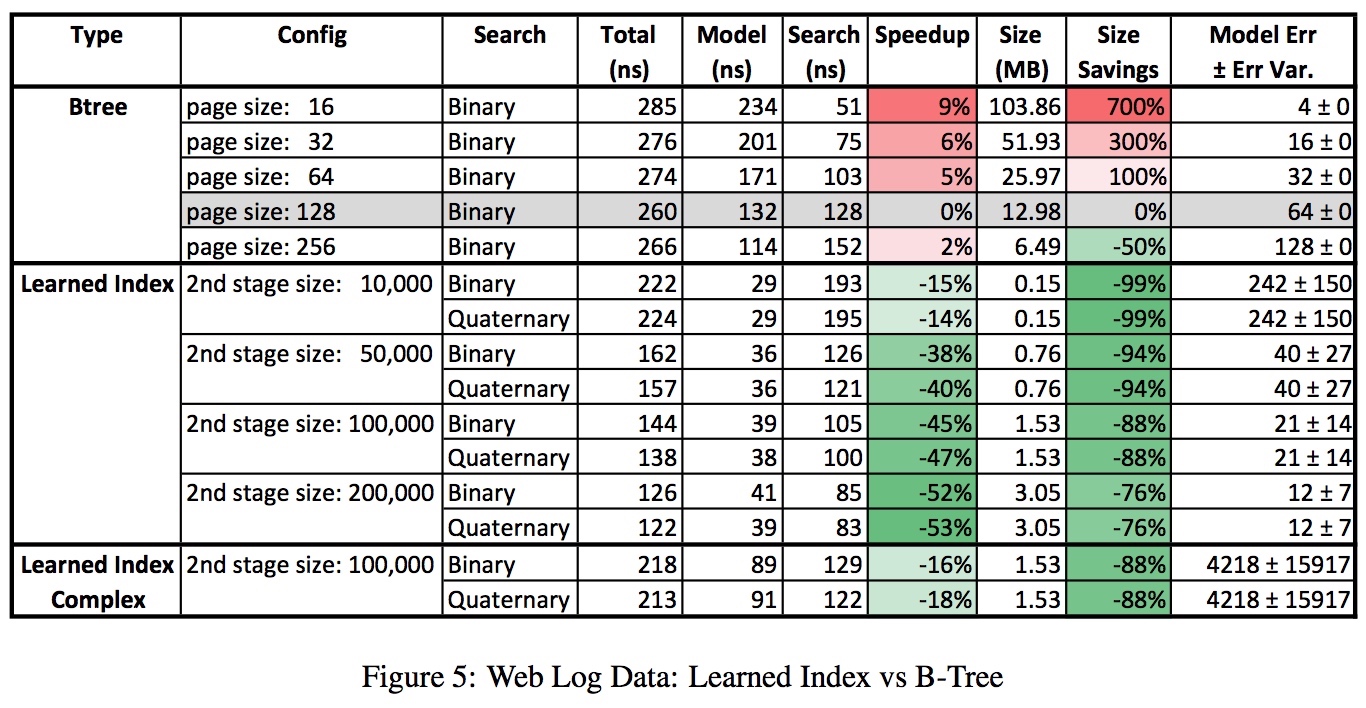
对于每个数据集,论文都给出了详细的测试结果,有兴趣的同学请看原文。
可以说是符合预期的,个人看法是:
- 因为算法 Step 3 的帮助,即使不经过调优,性能至少不输 B 树;
- 肯定能省下许多空间,因为 B 树是基于比较的查找,叶结点要保存 key 的内容,key 越多索引越大;而 NN 完全不受这个制约。
但暂且不要太激动,这只是查找性能。索引的维护(增/删/改)代价如何也是要考虑的。用作者原话说,这是 learned index 的阿喀琉斯之踵,因为 NN 模型的 retrain 代价是不可预测的,这是多数 ML 算法和传统算法一个很大的不同点。对此,作者意见如下:
- 如果恰好新的数据已经能被成功预测了,那就不用 retrain 了;但这太理想化,我们为达到 last mile 做的那些 overfitting 也导致了这个模型泛化性堪忧。
- 如果一定要 retrain,一个简单有效的优化是:把变更数据累积起来先放着,批量训练;
- 此外,retrain 可以借鉴一些 warm-start 的方法加快训练过程。
其他索引结构
论文中这部分没有详细展开,因为原理和前文几乎没有区别,仅仅换一种用法。
Point Index
拳打完 B 树再来脚踢 hash-map。大家都知道 hash-map 兼具 \(O(1)\) 的高效率和低效的空间使用率,想快就要减少碰撞,于是要牺牲更多的空间。所谓空间换时间。即使是 Google 的 Dense-hashmap 也会有 78% 的 overhead。
解决方案如图所示,用 RM-Index 模型替换掉 hash function。其思想是,利用数据的某些内在特征,帮助它找到一个最均匀(uniform)的映射方式,而不是用哈希彻底随机化。
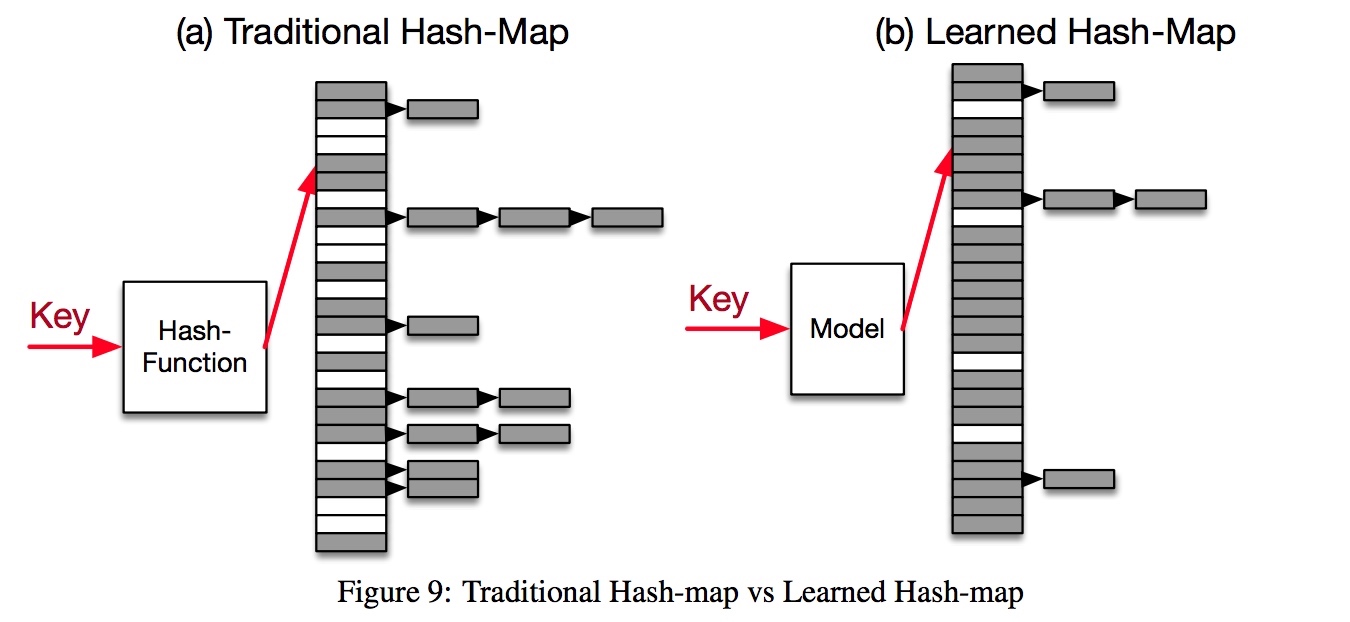
在三个数据集上的测试表明,这一方法的确提升了 slot 的空间利用率,减少了很多空 slot,减少的比例约 -6% ~ -78%。
Existence Index
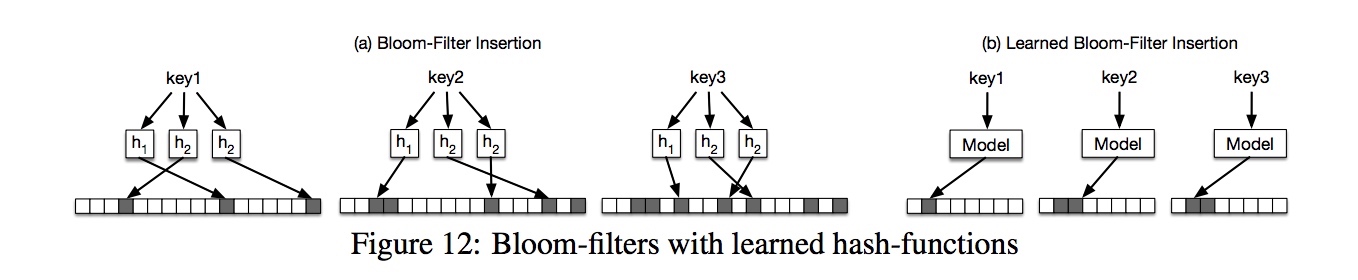
这回轮到的是 bloom filter,有两种思路:
- 直接用一个二分类模型判断是否存在;
- 和上一小节的原理类似,把 hash 函数替换成 RMI 模型。
后记
在 Jeff Dean 大神的光环之下,这篇文章很快引起热烈的讨论。
不得不说,这个脑洞开的很大,令人为之一振。一直在人们心中只能做“模糊”预测的 ML 算法竟然能代替经典的 B 树,放在 10 年前估计会被喷到体无完肤。
论文的亮点在于,大家一直在“训练——预测”这样一个思维下作 ML 而忽视了一点:至少对于已知的数据,ML 算法也是能输出一个确定的结果的!换句话说,在全集上训练,把错误率强行 bound 住其实很容易。
下面说说优缺点。
Learned index 对于规律性强的数据是大杀器,作这种数据的二级索引再合适不过了。内在规律越强,就意味着 B 树、哈希这些通用算法浪费的越多,这也是 ML 算法能捡到便宜的地方。
就像很多 DBMS 引入全文索引一样,未来的 DBMS 也也可以尝试给用户更多其他选项,为某些特别有规律的 column 建立非 B 树/Hash 的二级索引。甚至可以让 DMBS 智能化,自己尝试寻找一些规律,将 B 树索引透明的替换成其他索引。
缺点也是明显的:增删改代价难以控制,可想而知,对于规律性不那么明显的数据,这足以抹平它查找的速度优势。但我相信之后会有更多改进的 index 模型出现,把这个代价尽可能减少。
一句话总结个人看法:
B 树作为通用索引的地位仍然难以撼动,但特定数据场景下,learned index 将成为一个有力的补充。